Improving Verilog Four State Logic

How SeqiLog improves the distinction between uninitialized/metastable and "don't care" values

Dec 30, 2024

Introduction

Hardware-oriented data types are a powerful feature of Verilog RTL. Unlike in C, where the bits of builtin, integer data types can only take Boolean {0, 1} values, Verilog allows you to assign the bits of a variable to 0, 1, X, and Z.

From the SystemVerilog (IEEE 1800) 2017 standard, Section 6.3.1: Logic Values:

The SystemVerilog value set consists of the following four basic values:
0—represents a logic zero or a false condition
1—represents a logic one or a true condition
x—represents an unknown logic value
z—represents a high-impedance state
The values 0 and 1 are logical complements of one another.
When the z value is present at the input of a gate or when it is encountered in an expression, the effect is usually the same as an x value. Notable exceptions are the metal-oxide semiconductor (MOS) primitives, which can pass the z value.

There are two problems here:

What does “unknown logic value” mean?
Why is a “high-impedance state” important for RTL?

Starting with the first problem, there are at least two types of unknown values: 1) uninitialized or metastable, and 2) “don’t care”. It is important to make a distinction here, because these two categories should behave differently in simulation. The former are values that should always propagate pessimistically from inputs to outputs for debug and correctness checking. The latter are values that should always propagate optimistically from inputs to outputs, because the designer leaves them unspecified on purpose. Verilog’s problem is that unless you pay for extra “X Prop” licenses from an EDA vendor, both uses of x have identical simulation semantics. We’re only getting one x for the price of two (actually three if you count Synopsys VCS tmerge, vmerge, and xmerge modes)!

Moving to the second problem, high impedance values operate at a lower level of abstraction than register transfer level (RTL) design and verification code. The IEEE 1800-2017 description paragraph says “at the input of a gate … the effect is usually the same as an x value”. The listed exception is a MOS primitive. Gates, MOS primitives, and even the concept of impedance—the measure of opposition to current flow—are circuit design concerns. The RTL abstraction is concerned with the legal input/output values of registers. If we follow Uncle Dijkstra’s advice and separate concerns appropriately, the z encoding is not pulling its weight.

In this post, we will start with a primer on Verilog X propagation rules. We will then dive deeper into the importance of pessimistic versus optimistic X propagation. Finally, we will explain SeqiLog’s humble proposal for fixing this costly and error-prone situation:

Drop z.
Split x into:
- pessimistic X, and
- optimistic “don’t care”, DC.

Primer on Verilog X Propagation

Let’s review how Verilog models hardware behavior with unknown values. This primer only focuses on logical ops, ternary ops, and control flow statements. For the complete picture, see a recent version of the SystemVerilog spec. Expert readers can skip this section.

Logical Ops

Start with Boolean NOT, OR, AND, and XOR functions:

Verilog Logic Operator Input/Output Values

Notice a few things:

Input z values never propagate to outputs.
OR outputs are dominated by 1 on any input.
AND outputs are dominated by 0 on any input.

Both OR and AND functions can terminate propagation of x/z from inputs to outputs. This is referred to as “optimistic” X propagation. The simulator uses Boolean Algebra identities (a|1==1 and a&0==0) to optimistically bias outputs to known values.

Ternary Ops

The following figure shows all 64 input/output mappings of the Verilog ternary (s?a:b) operator:

Notice a few things:

When s is either 0 or 1, any input—including z—propagates directly to the output.
When s is either x or z, if a==b, the output will equal a.
When s is either x or z, input z values never propagate to outputs.

Perhaps surprisingly, the result of a ternary operator s?a:b will NOT always equal the result of s&a|~s&b, despite being logically equivalent.

The x?a:a => a and z?a:a => a results are another form of optimistic X propagation. Even though this 2:1 multiplexor has an x/z on its select (s) input, the simulator uses a Boolean identity (s&a|~s&a <=> a) to optimistically bias outputs to known values.

Control Flow Ops

A novice Verilog coder might think the following blocks are equivalent:

// Block 1: Ternary
always_comb begin
    y = s ? a : b;
end

// Block 2: If / Else
always_comb begin
    if (s) y = a;
    else   y = b;
end

Block #2 will behave according to the following table:

They are only equivalent if the input s is in {0, 1}. If s is in {x, z}, block #2 will always output b. That’s because the Verilog if statement treats x/z as False.

This is yet another form of X optimism. In this case, it doesn’t bias the outputs to known values. Rather, it biases outputs to whatever value is specified in the else branch. In this case, it biases the outputs to b.

For this reason, most people prefer to use a variation of Verilog case statement for selection logic:

// Block 2: If / Else
always_comb begin
    unique case (s)
        1'b1: y = a;
        1'b0: y = b;
        default:
            y = 'x;
    endcase
end

Important X Use Cases

Uninitialized State

By far the most important use of Xes in simulation is the initial value for state variables. For example, flip flops and SRAMs should all start in an unknown state at time zero.

Flips flops used in control logic such as finite state machines should be explicitly reset to a known value. Flip flops used in data path logic typically do not have resets. A reset network is large and expensive; it would waste too much area and power to explicitly reset every flop in the design.

SRAMs are used for medium-to-large storage of data. They are designed for density, and do not contain explicit reset circuitry. Unlike flip flops, SRAM cell values cannot be accessed directly on any given clock cycle. Setting SRAM state requires a write operation, and getting SRAM state requires a read. The design/verification engineer should expect an SRAM read from address A to return unknown values if there has not been an antecedent write to address A.

In general, X values from uninitialized state should propagate pessimistically to outputs and observable interfaces. The primary reasons are 1) functional correctness, and 2) debug efficiency.

Control logic should always and forever be completely deterministic. If a finite state machine ever uses one bit of input from uninitialized state, it should produce a failure in simulation. Optimistic X propagation introduces the possibility that control logic might silently use uninitialized state without reporting an error. Therefore, optimistic X propagation—the default Verilog behavior—should be regarded with intense paranoia.

Experienced digital designers love X values, because they simplify debug. If all state is initialized to random values, you need to track down the exact 0/1 mismatch somewhere in the waveform debugger tool. Xes on the other hand are painted bright red like a flashing traffic light. Finding the X is easier than finding a mismatch, which saves time and money. On a side note, this is a surprising limitation of Verilator, the most commonly used open source RTL simulation tool.

Multi Cycle Paths

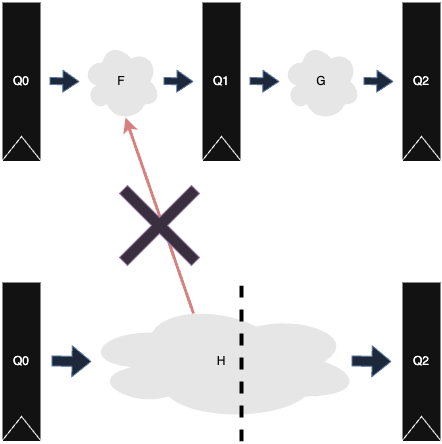
A slightly less common, but equally important category of X propagation issues is multi cycle paths. The following figure shows a circuit with a multi cycle path:

The logic in F and G clouds executes in a single cycle, but the logic in H cloud is designed to complete in two clock cycles, a multi cycle path (MCP). Using H as shown violates the setup time of Q1, which could lead to unpredictable and possibly metastable results.

The best way to deal with MCPs is to ban them entirely. They add complexity to design, verification, synthesis, and place-and-route. They are known to cause catastrophic bugs.

However, if you must use an MCP, the best known method for finding designer mistakes is to force the value of H to X until the last cycle of the MCP. It is essential for this X to reach Q1 in order to detect the error, so X optimism is highly undesirable.

Don’t Care Values

One last use case for Xes in HDL design and verification is “don’t care” values. If you think back to your first Karnaugh Map in Digital Design 101, remember that placing an X in one of the cells means that this value could be 0 or 1. The X in a cell can be used to reduce the number of minterms in the cover.

This type of unspecified value is also called “don’t care” in the Espresso logic minimizer project PLA file format. See Multiple-Valued Logic Minimization for PLA Synthesis by Richard Rudell for details.

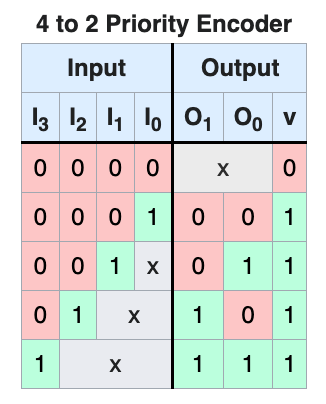
A simple example is the priority encoder described here:

The values of O[1:0] are known if v==1, but otherwise they are “don’t care”. If the inputs are all zeros, this particular encoding is “invalid”, and therefore the output index has no meaning. The designer could hard code the values of O[1:0] to zeros, but leaving it unspecified allows more degrees of freedom for the logic minimization tool to optimize.

This is a case where X optimism is exactly what we want. The value of O[1:0] will only be used if v==1, and therefore squashing its propagation is required.

Brief Recap

We have now established the following:

Verilog only supports X optimism.
There are compelling reasons to support both X optimism and pessimism in simulation.

Now let’s see how SeqiLog approaches the problem.

SeqiLog Solution

As mentioned above, SeqiLog attempts to thread the needle by 1) dropping z, and 2) enabling the design/verification engineer to choose whether a value should propagate Xes in simulation.

Logical Ops

Execute the following Python code to see a complete truth table of SeqiLog logic functions:

Note that SeqiLog’s string literal notation for X is capital “X”, and DC is “-”. The DC dash character is taken from Espresso PLA format.

The following figure shows a graphical summary of the outputs. Note that for clarity, we have replaced “DC” with w. Think of w as meaning “a weak form of x”.

SeqiLog Logic Operator Input/Output Values

To contrast this with Verilog logic operators:

It is possible for all four values to propagate to outputs.
The OR function 1 input dominates DC, but does NOT dominate X.
The AND function 0 input dominates DC, but does NOT dominate X.

This is a more balanced approach. Both optimistic (with DC) and pessimistic (with X) unknown propagation is supported. And since “high impedance” isn’t relevant to anything, it doesn’t occupy any mindshare.

Ternary Ops

Even though Python has conditional expressions, they are not overloadable. Instead, SeqiLog implements an ite (if-then-else) function with the following input/output values:

Aside from not supporting z, the only difference from Verilog’s ternary operator is how ite implements X pessimism. If X appears on any of its inputs, the output becomes X.

Control Flow Ops

Verilog is its own language, but SeqiLog is a meta-HDL implemented in Python. Therefore, it must work within Python constraints.

Python’s if statement attempts to determine the “truthiness” of the argument. The standard way of doing this is for Python objects to implement a __bool__ method. In SeqiLog, all known bits objects can be evaluated for truthiness by converting to an unsigned int, but unknown bits objects raise a ValueError.

>>> if bits("1b1"):
...     print("Hello!")
Hello

>>> if bits("1bX"):
...     print("Hello!")
...
ValueError: Cannot convert unknown to uint

It is therefore technically possible to write SeqiLog functions use Python if statements, but you must guarantee all the inputs are known ahead of time. Since this falls short of hardware design/verification requirements, we need to use the Python match statement instead:

>>> def foo(x: Vec[1]):
...     match x:
...         case "1b0":
...             print("Hello zero")
...         case "1b1":
...             print("Hello one")
...         case "1b-":
...             print("Hello DC")
...         case "1bX":
...             print("Hello X")
...         case _:
...             assert False

>>> foo(bits("1b0"))
Hello zero
>>> foo(bits("1b1"))
Hello one
>>> foo(bits("1b-"))
Hello DC
>>> foo(bits("1bX"))
Hello X

SeqiLog’s solution for the limitations of if/else is similar to Verilog’s: prefer using case statements. Both support X propagation, but SeqiLog allows the designer to implement separate branches for optimistic and pessimistic X propagation.

Conclusions

Verilog’s four state logic is antiquated for modern RTL design. There is no need for a z “high impedance” state, and it’s default X optimism can lead to suboptimal results for design/verification functional correctness and debug.

In this post, we briefly reviewed a subset of Verilog’s defined behavior when handling unknown values in simulation. We then contrast them with SeqiLog’s alternatives.

SeqiLog is an experimental Python meta-HDL. At the time of this writing, it is not an alternative to Verilog. Not even close. But it’s a fun hobby project. We hope to spur innovation in this space, and better X propagation is a great place to start.

Fuzzy Logic

Discussion about this post